Think Outside the Policy: In-Context Steered Policy Optimization

ArXiv URL: http://arxiv.org/abs/2510.26519v1
作者: Yunfang Wu; Saiyong Yang; Chenming Tang; Hsiu-Yuan Huang; Weijie Liu
发布机构: Peking University; Tencent

TL;DR

本文提出了一种名为“上下文引导策略优化” (In-Context Steered Policy Optimization, ICPO) 的新型强化学习框架，该框架利用大推理模型 (Large Reasoning Models, LRM) 固有的上下文学习 (In-Context Learning, ICL) 能力，仅通过现有数据集生成专家指导，从而在不依赖更强专家模型的情况下，有效提升模型的探索范围和推理性能。

关键定义

本文提出或沿用了以下对理解论文至关重要的核心概念：

上下文引导策略优化 (In-Context Steered Policy Optimization, ICPO): 本文提出的统一强化学习框架。它通过“隐式专家强制”来利用模型的上下文学习能力，生成高质量的探索轨迹，并结合“专家区域拒绝采样”和“退火专家奖励塑造”技术来稳定训练过程，从而提升大推理模型的性能。
隐式专家强制 (Implicit Expert Forcing, IEF): ICPO 的核心机制。它不依赖于一个外在的、更强的专家模型，而是通过在模型的输入中提供少量高质量的示例（few-shot ICL），来“隐式地”引导当前模型生成偏向专家行为的轨迹。这些轨迹被用作异策略 (off-policy) 数据，以扩大探索空间。
专家区域拒绝采样 (Expert Region Reject Sampling, ERRS): 一种为稳定训练而设计的过滤机制。它定义了一个“专家区域”，即只有那些通过 IEF 生成且奖励高于预设阈值的“高质量”轨迹才会被接纳并用于模型更新，从而防止低质量或有噪声的轨迹对策略优化产生负面影响。
退火专家奖励塑造 (Annealed Expert-Bonus Reward Shaping, RS): 一种奖励调整策略。它在训练早期为被采纳的专家轨迹提供一个额外的、随训练步数线性衰减的奖励加成。这旨在训练初期鼓励模型模仿专家行为，而在后期逐渐减少依赖，促进模型自主优化。
组相对策略优化 (Group Relative Policy Optimization, GRPO): 本文方法所基于的一种高效的强化学习优化算法。它通过对一批轨迹（一个组）的奖励进行归一化来计算优势函数，避免了使用额外的价值网络，适用于大语言模型。

本文方法

本文提出了一个名为 ICPO 的统一强化学习框架，其核心思想是利用模型自身的上下文学习能力来生成专家指导，从而避免了对外部专家模型的依赖。该框架主要包含三个关键组件：隐式专家强制 (IEF)、专家区域拒绝采样 (ERRS) 和退火专家奖励塑造 (RS)。

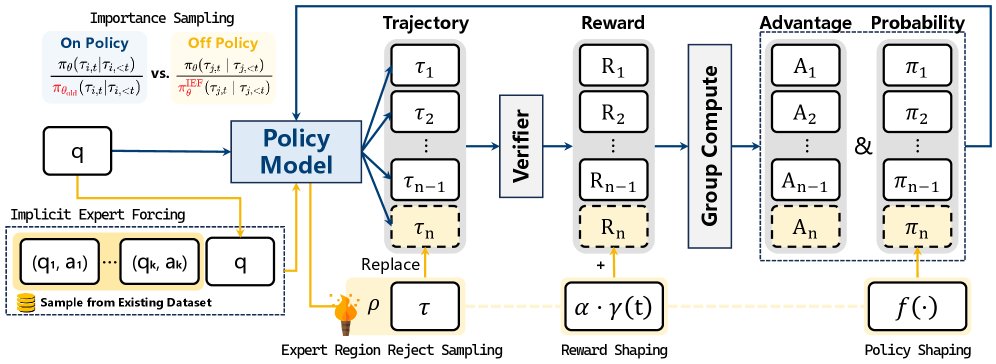
用 Few-Shot ICL 实现隐式专家强制

传统方法依赖“显式专家强制”，即通过模仿学习或KL散度约束，使当前策略对齐一个独立的专家模型 $\pi_{\phi}$，这需要梯度计算和额外的专家模型。

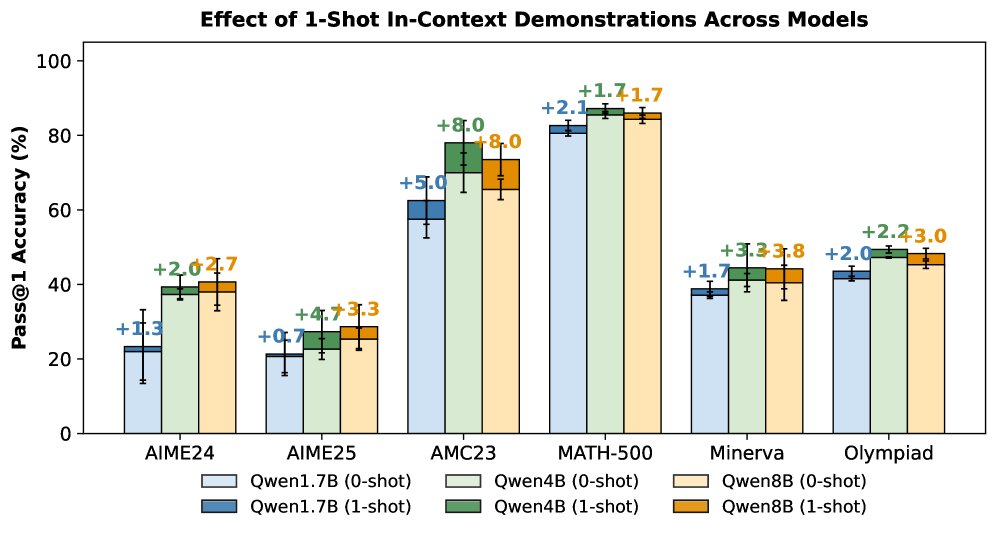
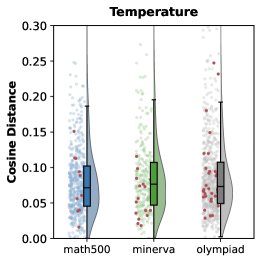
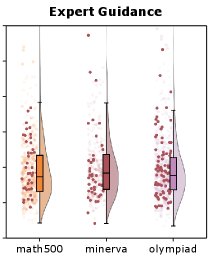
本文发现，小样本上下文学习 (Few-shot ICL) 本身就是一种有效的、无梯度的专家条件推理方式。通过在输入中加入高质量的示例，模型的输出分布会向专家行为靠拢，从而产生更高质量和更多样化的轨迹。 $0-shot $\!\rightarrow\!$ 1-shot (t=0.6)$

这种由 ICL 引导产生的策略分布可被形式化为：

\[\pi_{\theta}^{\text{IEF}}(\tau\mid q):=\pi_{\theta}(\tau\mid[\mathcal{D};q])=\pi_{\mathcal{F}}(\tau\mid q;\vartheta)\]

其中，$\mathcal{D}$ 是上下文示例，它隐式地生成了一个编码专家行为的任务向量 $\vartheta$。这相当于在不修改模型参数 $\theta$ 的情况下，引导模型生成“专家级”的输出，本文将此过程称为 隐式专家强制 (IEF)。

混合策略 GRPO

为了将 IEF 产生的专家级探索融入训练，ICPO 扩展了 GRPO 算法，构建了一个 混合策略 (Mixed-Policy) GRPO。在每次迭代中，模型会生成 $N_{\text{on}}$ 条同策略轨迹 $\tau_{i}\sim\pi_{\theta_{\text{old}}}$ 和 $N_{\text{off}}$ 条通过 IEF 生成的异策略轨迹 $\tau_{j}\sim\pi_{\theta_{\text{old}}}^{\text{IEF}}$。

所有这些轨迹的奖励被放在一起进行组归一化，以计算优势函数 $\hat{A}_{i}$：

\[\hat{A}_{i}=\frac{R(\tau_{i})-\text{mean}(G_{\text{on}}\cup G_{\text{off}})}{\text{std}(G_{\text{on}}\cup G_{\text{off}})}\]

混合策略的目标函数结合了同策略和异策略两部分：

\[\begin{aligned} \mathcal{J}_{\scriptscriptstyle\text{Mixed}}(\theta) &= \underbrace{\mathbb{E}_{\tau\sim\pi_{\theta_{\text{old}}}}}_{\text{on-policy}}\Bigg[\frac{1}{ \mid \tau \mid }\sum_{t=1}^{ \mid \tau \mid }\operatorname{CLIP}\big(r_{t}(\theta),\,\hat{A}(\tau),\,\epsilon\big)\Bigg] \\ &\quad+\underbrace{\mathbb{E}_{\tau\sim\pi_{\theta_{\text{old}}}^{\text{IEF}}}}_{\text{off-policy}}\Bigg[\frac{1}{ \mid \tau \mid }\sum_{t=1}^{ \mid \tau \mid }\operatorname{CLIP}\big(\hat{r}_{t}(\theta),\,\hat{A}(\tau),\,\epsilon\big)\Bigg], \end{aligned}\]

这使得模型既能在当前策略附近进行微调（利用），也能朝 IEF 指引的专家区域进行探索。这种方法是“自给自足”的，因为它仅使用当前模型 $\pi_{\theta}$ 和现有数据集，无需外部专家模型。

专家区域拒绝采样 (ERRS)

为了防止低质量的 IEF 轨迹干扰训练，ICPO 引入了 专家区域拒绝采样 (ERRS)。首先定义一个“专家区域” $\mathcal{E}_{\text{exp}}$，只包含那些由 IEF 生成且奖励值高于特定阈值 $\delta$ (默认为1.0) 的轨迹：

\[\mathcal{E}_{\text{exp}}=\big\{(x_{\text{exp}},\tau_{j})\ \big \mid \ R(\tau_{j})>\delta\big\}\]

然后，通过一个拒绝采样算子 $\rho$，确保只有落入该专家区域的轨迹才对异策略部分的损失函数有贡献。这有效过滤了噪声，保证了更新方向的可靠性。最终的 ICPO 目标函数为：

\[\begin{aligned} \mathcal{J}_{\mathrm{ICPO}}(\theta)=\frac{1}{Z}\Big( &\underbrace{\sum_{i=1}^{N_{\mathrm{on}}}\sum_{t=1}^{ \mid \tau_{i} \mid }\mathrm{CLIP}(r_{i,t}(\theta),A_{i},\epsilon)}_{\text{on-policy objective}} \\ +&\underbrace{\rho\!\left(\sum_{j=1}^{N_{\mathrm{off}}}\sum_{t=1}^{ \mid \tau_{j} \mid }\mathrm{CLIP}(f(\hat{r}_{j,t}(\theta)),\hat{A}_{j},\epsilon)\right)}_{\text{off-policy objective}}\Big), \end{aligned}\]

退火专家奖励塑造 (RS)

为了在训练早期更强地引导模型模仿专家行为，ICPO 引入了 退火专家奖励塑造 (RS)。对于那些被 ERRS 采纳的、且答案正确的专家轨迹，其奖励会被赋予一个额外的、随训练步数线性衰减的奖励加成：

\[R_{\text{shaped}}(\tau)=R(\tau)+\alpha\cdot\gamma(t)\]

其中，$\gamma(t)=1-\frac{t}{T}$ 是线性衰减调度器，$t$ 是当前训练步数，$T$ 是总步数。这种设计在初期强化专家引导，后期则逐渐放手，让模型自主优化，从而在稳定性和探索性之间取得平衡。

ICPO 训练流程

ICPO 的完整训练流程如下：

采样提示: 从数据集中采样一批提示 (prompts)。
生成轨迹:
- 同策略: Для каждого подсказки, генерируется $N_{\text{on}}$ траекторий с помощью текущей политики $\pi_{\theta_{\text{old}}}$.
- 异策略 (IEF): 从 MATH 数据集中随机抽取 $k$ 个示例，与提示一起构建上下文，然后用 $\pi_{\theta_{\text{old}}}$ 生成一条 IEF 轨迹 $\tau^{\text{IEF}}$。
专家区域过滤与奖励塑造:
- 检查 IEF 轨迹 $\tau^{\text{IEF}}$ 是否正确且奖励大于阈值 $\delta$。
- 如果满足条件，则随机替换一条同策略轨迹，并为其添加退火奖励加成。
计算损失与更新:
- 使用混合后的轨迹集，根据公式计算组归一化优势 $\hat{A}$。
- 根据最终的 ICPO 目标函数 $\mathcal{J}_{\mathrm{ICPO}}(\theta)$ 计算总损失。
- 执行梯度下降更新模型参数 $\theta$。
更新旧策略: 将 $\pi_{\theta_{\text{old}}}$ 更新为 $\pi_{\theta}$，为下一轮迭代做准备。

实验结论

实验在 Qwen3-1.7B 和 Qwen3-8B 模型上进行，并与基线方法 GRPO 和 LUFFY (使用外部专家模型) 进行了比较。

主要结果

总体性能提升: 在分布内 (in-distribution) 的数学推理基准测试中，ICPO 及其变体 ICPO†（包含奖励塑造RS）在两种模型规模上均显著优于基线 GRPO。例如，在 Qwen3-8B 模型上，ICPO 和 ICPO† 分别带来了 2.02 和 2.75 个百分点的平均性能提升。

模型 (Qwen3-8B)	NuminaMath	R1-M Hard	MATH	GSM8K	R1-M Easy	平均	OPs/tok
GRPO	91.00	54.79	38.54	83.75	50.74	62.37	63.53
ICPO	92.00	55.21	43.65	86.95	51.10	65.78	66.86
ICPO†	92.00	56.15	40.94	92.00	51.47	66.51	67.06

奖励塑造 (RS) 的效果: ICPO† 在专家域数据集 (NuminaMath) 上表现尤为出色，证明了 RS 能够有效加强模型与专家行为的对齐。
分布外 (OOD) 泛化能力: 在 OOD 基准测试中，ICPO† 同样保持了与 GRPO 相当或更优的性能，表明该方法在增强特定领域能力的同时，没有损害模型的通用推理能力。
训练稳定性: 奖励曲线图显示，ICPO 及其变体在整个训练过程中始终能获得比 GRPO 更高的奖励，表明其优化过程更稳定、更高效。

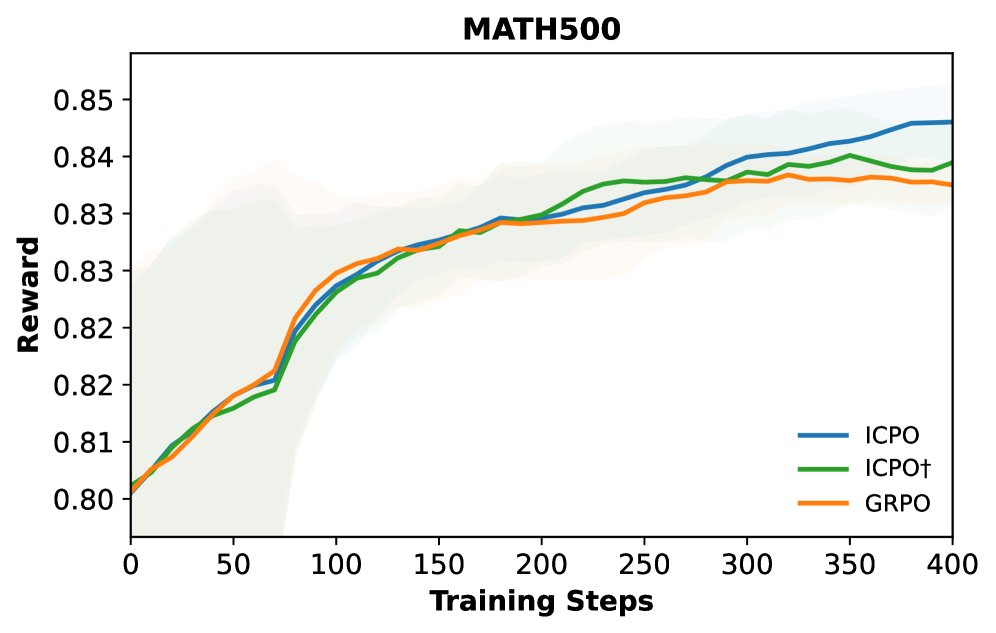
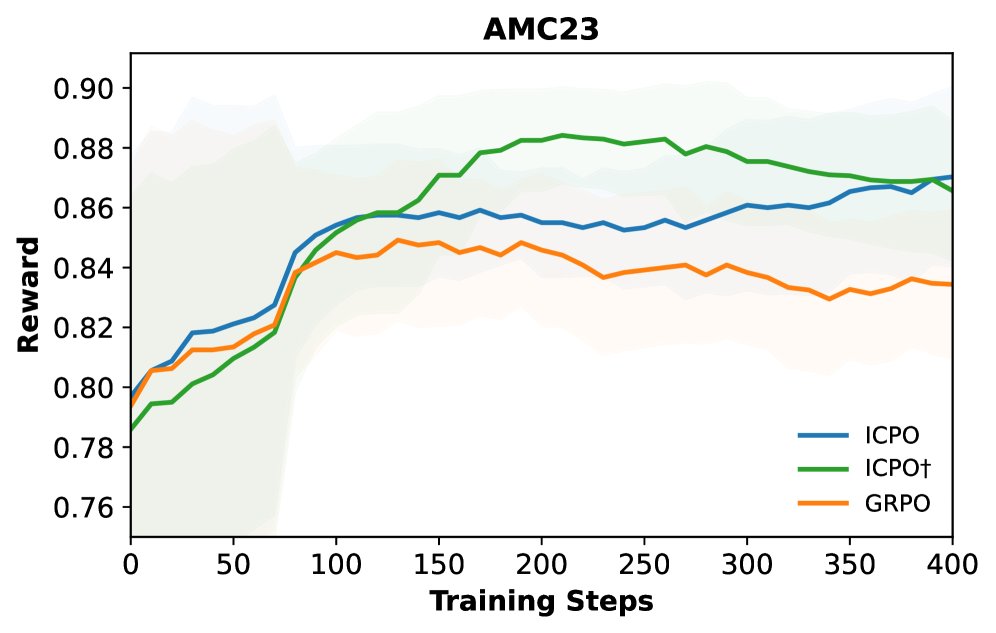
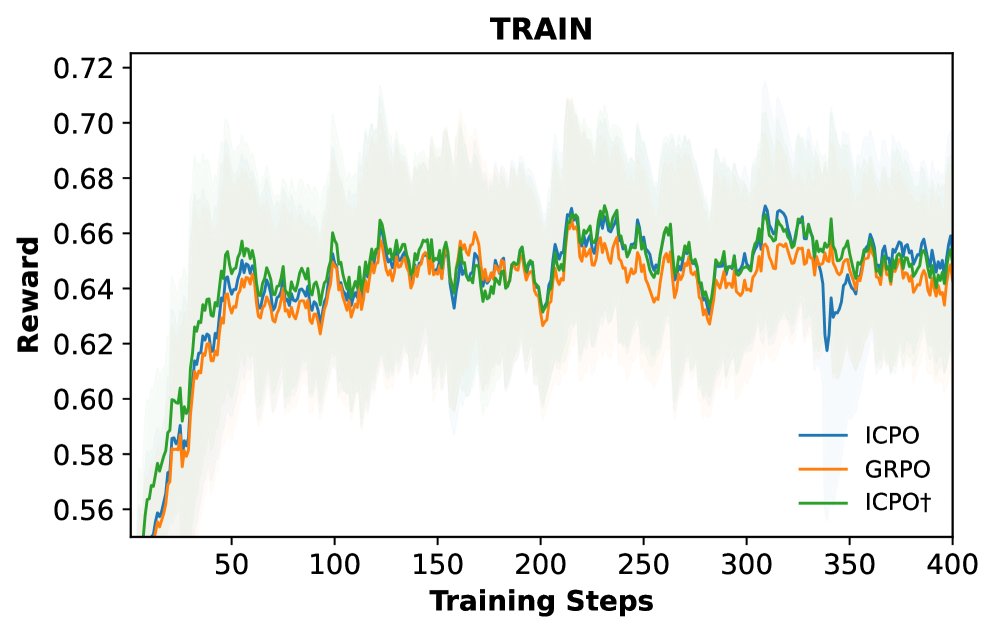
消融研究与分析

各组件的贡献: 逐个移除 ICPO† 的三个组件（IEF、ERRS、RS）后，模型性能均出现下降。其中，IEF 带来了最大的性能增益，证明了利用 ICL 进行专家引导是该框架最核心、最有效的创新。ERRS 和 RS 则分别在过滤噪声和稳定优化方面起到了关键的补充作用。

方法 (Qwen3-8B)	NuminaMath	R1-M H./Mnrv.	GSM8K	R1-M Easy	平均
ICPO†	92.00	56.15 / 40.94	92.00	51.47	66.51
- RS (即 ICPO)	92.00	55.21 / 43.65	86.95	51.10	65.78
- ERRS	89.60	55.21 / 41.67	85.16	53.31	64.99
- IEF (即 GRPO)	91.00	54.79 / 38.54	83.75	50.74	63.76

与外部专家模型的比较: 与依赖先进 LRM 生成轨迹的 LUFFY 方法相比，ICPO 在不使用任何外部模型的情况下，仅凭 IEF 就取得了更优的性能，证明了 ICPO 是一种成本效益更高、更具可扩展性的方案。
对不同难度数据的泛化性: 实验表明，无论是在简单的还是困难的推理数据集上进行训练，IEF 都能稳定地提升 GRPO 的性能，证明了该方法的普适性。

总结

实验结果有力地证明，ICPO 是一个可扩展且高效的 RLVR 范式。它通过巧妙地利用模型固有的上下文学习能力，成功地解决了传统 RL 方法在探索上的局限性，并且无需依赖昂贵且不易获取的外部专家模型，为大推理模型的后训练提供了一条新的有效路径。