Tree Training: Accelerating Agentic LLMs Training via Shared Prefix Reuse

TL;DR

本文提出了一种名为 Tree Training 的新训练范式，通过将智能体交互产生的树状轨迹数据进行高效打包和计算复用，在训练的前向和后向传播中对共享的前缀（prefix）只计算一次，从而显著提升了智能体大语言模型（Agentic LLM）的训练效率。

关键定义

相关工作

在智能体大模型的应用场景中，模型的交互过程常常呈现出分支行为。例如，树状规划、并发工具调用或记忆检索等机制都会导致单一任务的token轨迹从线性序列演变成树状结构。

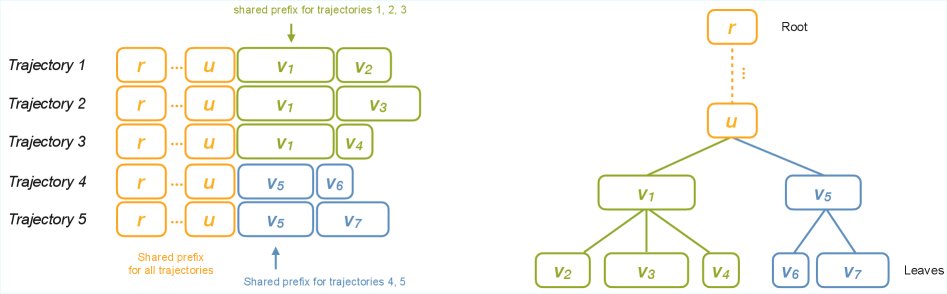
Refer to caption

当前主流的训练流程通常会将这种树状轨迹分解成多个独立的线性片段进行处理，导致不同分支间的共享前缀在训练的前向和后向传播中被反复计算，带来了巨大的计算和内存冗余。这在大型监督微调（SFT）或强化学习（RL）中严重限制了训练吞吐量。

虽然已有研究在强化学习的生成阶段利用共享前缀来提升采样效率，但这些方法在训练阶段仍将轨迹视为独立样本，未能解决训练过程中的计算冗余问题。一个直接的想法是复用前向传播中的KV缓存，但这在反向传播中是行不通的，因为前缀的梯度依赖于其后的整个序列，简单缓存无法保证梯度的正确性。

因此，本文旨在解决的核心问题是：如何设计一种新的训练框架，能够在训练的前向和后向传播中高效地复用树状轨迹中的共享前缀计算，同时保证数学上的完全等价性，从而消除计算冗余，加速智能体模型的训练。

本文方法

概述

为了解决共享前缀在反向传播中因后续序列不同而导致梯度不一致的问题，本文提出了 Tree Training 范式。其核心思想是在一个微批次（micro-batch）内同时处理共享前缀及其所有后续分支。这样，在计算反向梯度时，可以获得计算所需的所有信息，同时确保共享部分的计算只进行一次。

如下图所示，对于两个共享前缀的序列，传统的KV缓存方法在前向传播中有效，但反向传播时，$dV_1$ 和 $dV_1’$ 的值因分别依赖于 $P_{21}$ 和 $P_{31}$ 而不同，导致简单的缓存机制失效。

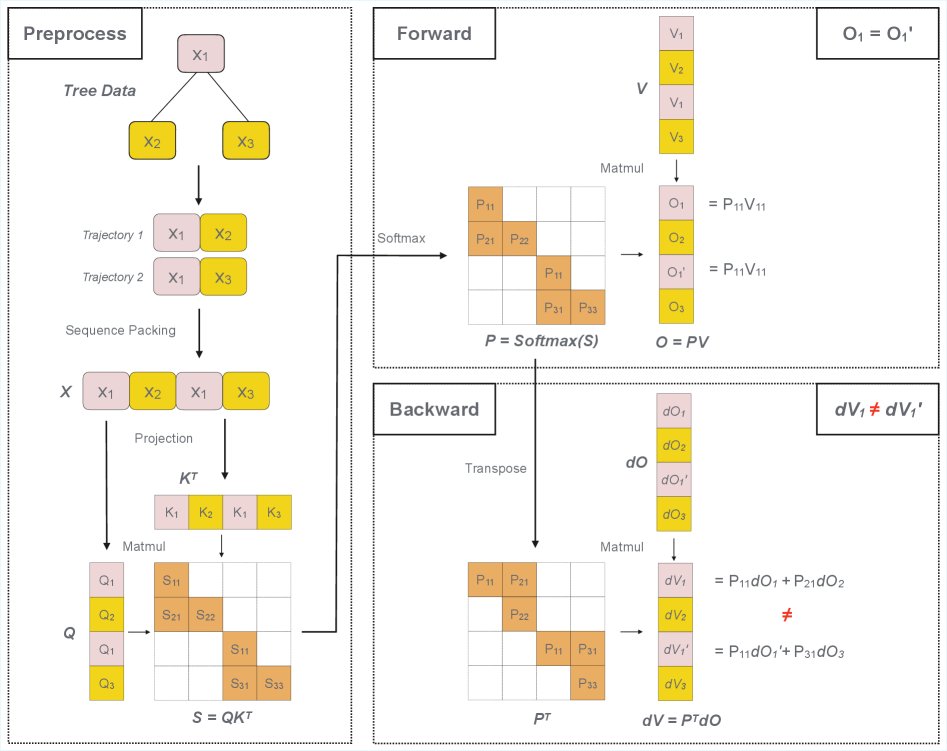
Refer to caption

本文的解决方案通过将它们打包在同一批次中来解决此问题，确保 $P_{11}$ 只计算一次，同时可以准确地计算和恢复 $dV_1$ 和 $dV_1’$ 的梯度。为了管理这种打包带来的内存增长，本文设计了 Tree Packing 算法。

atención 操作的前向传播可表示为：

\[\begin{gathered}S=Q\times K^{T}\\ P=\mathrm{softmax}(S)\\ O=P\times V\end{gathered}\]

其反向传播中 $dV$ 的计算可表示为：

\[\begin{gathered}dV=P^{T}\times dO\end{gathered}\]

Tree Packing

Tree Packing 的目标是将整个计算树划分为适合GPU内存容量的子树，并通过优化划分策略来最大化共享前缀的复用。

Refer to caption

单路径打包 (Single-Path Packing)

这是一种简化的场景，假设每个训练步骤只选择树中的一条路径作为共享前缀。此问题可以通过动态规划（Dynamic Programming）解决。

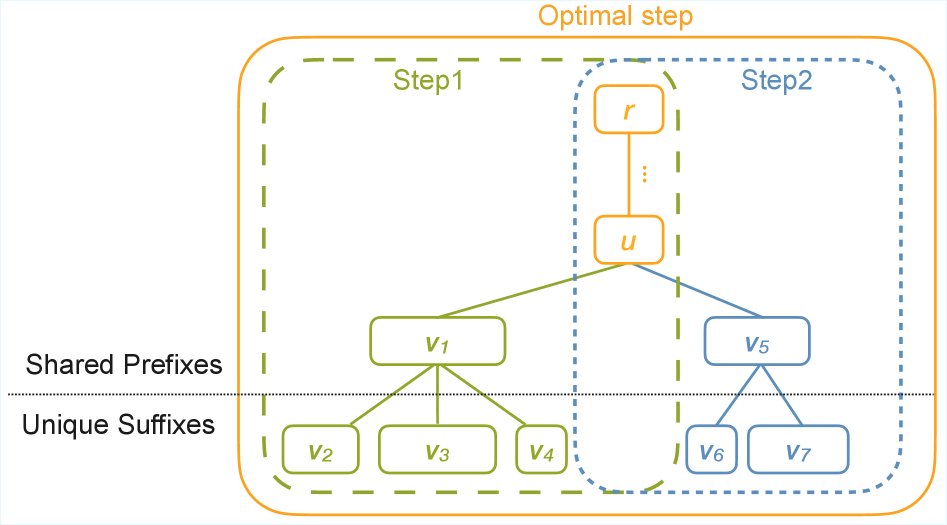
多路径打包 (Multi-Path Tree Packing)

单路径打包策略可能不是最优的，因为在容量允许的情况下，同时打包多个共享路径（形成层级共享结构）可以获得更大的计算节省，如上图 Figure 3 所示。多路径打包将此问题推广，允许在一个训练步骤中激活多个共享路径。

该问题被建模为一个更复杂的动态规划，其中每个节点的状态表示为一组候选的（容量占用向量，成本）对。父节点的状态通过对其子节点的状态进行两种操作来构建：

  1. 提升 (Lift)：将子节点的状态向上层传播，并累加上连接边的长度。
  2. 装箱 (Bin packing)：将所有子节点提升来的需求（items）组合打包到容量为 $C$ 的“箱子”中，这是一个NP-hard问题。

由于其高复杂性，精确的多路径DP算法仅适用于中小型树。在实践中，本文采用了一种高效的启发式算法，其遵循三个原则：

  1. 优先分配最深的叶节点。
  2. 将相似深度的叶节点组合在一起以提高打包效率。
  3. 以深度优先的顺序遍历树，当累积长度超过容量时启动新的遍历。

Gradient Restoration

在前向传播中，由于有因果掩码（causal mask），共享前缀的计算结果在所有共用它的序列中都是相同的。然而，在反向传播中，非前缀部分（后缀）的token会对前缀token贡献梯度，导致前缀的梯度在不同序列间不再相同。

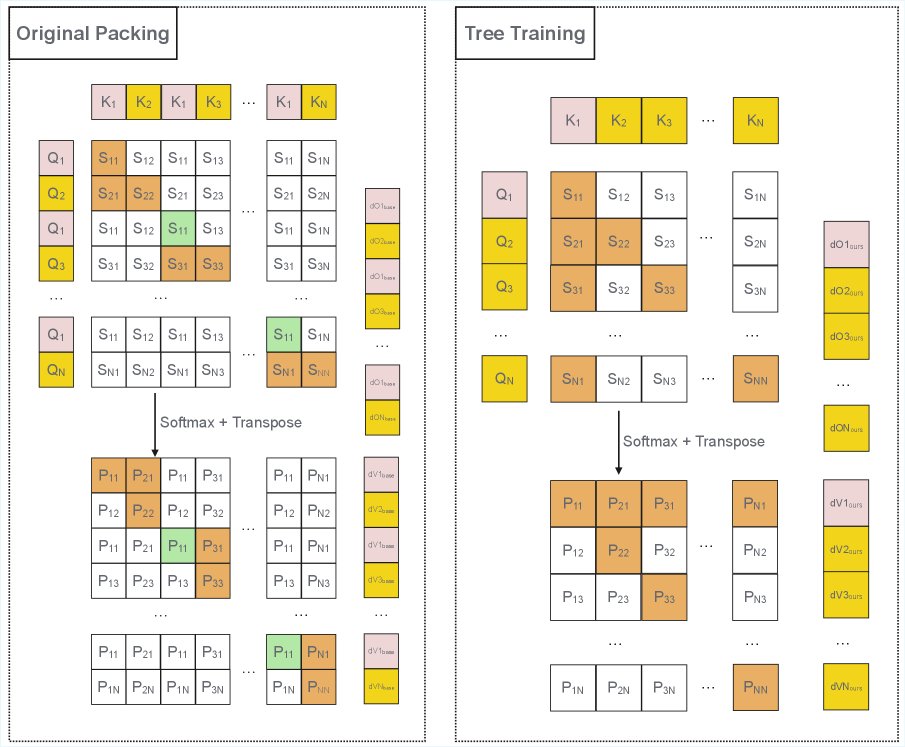
Refer tocaption

梯度恢复的核心挑战是：如何在只计算一次共享前缀的情况下，保证最终的梯度更新与独立计算所有完整序列时完全等价。

参数更新与梯度

对于一个线性变换 $Y=X \cdot \text{weight}$，其权重梯度为 $d\text{weight}=X^{T} \cdot dY$。假设我们有 $n$ 条轨迹共享前缀 $P$，各自拥有后缀 $S_i$。

为了保证权重梯度等价，我们需要确保前缀 $P$ 对梯度的总贡献相同，即：

\[P^{T}\times dY_{P}^{ours}=P^{T}\times(\sum_{i=1}^{n}dY^{base}_{p_{i}})\]

由于 $P$ 是相同的，这等价于要求：

\[dY_{P}^{ours}=\sum_{i=1}^{n}dY^{base}_{p_{i}}\]

同时，后缀部分的梯度需要保持不变：

\[dY_{S_{i}}^{ours}=dY_{S_{i}}^{base},\forall i\in[1,n]\]

算法分析

本文通过分析证明，对于Transformer中的主要操作（如线性变换、Attention等），上述梯度累加的性质是可传递的。

这个传递性意味着，我们只需要在反向传播链的起始处进行一次梯度校正，这个校正效果就会自动传播到整个模型。

实现

Refer to caption

  1. 共享前缀注意力掩码 (Shared Prefix Attention Mask): 在前向传播中，使用一个定制的注意力掩码，确保不同分支的token不会注意到彼此，从而安全地共享前缀表示。本文基于FlashAttention V3实现了高性能的GPU内核。
  2. 位置嵌入 (Position Embedding): Tree Packing改变了token的物理位置，因此需要一个机制来恢复每个token在原始轨迹中的位置ID，以确保像RoPE这类位置敏感操作的正确性。
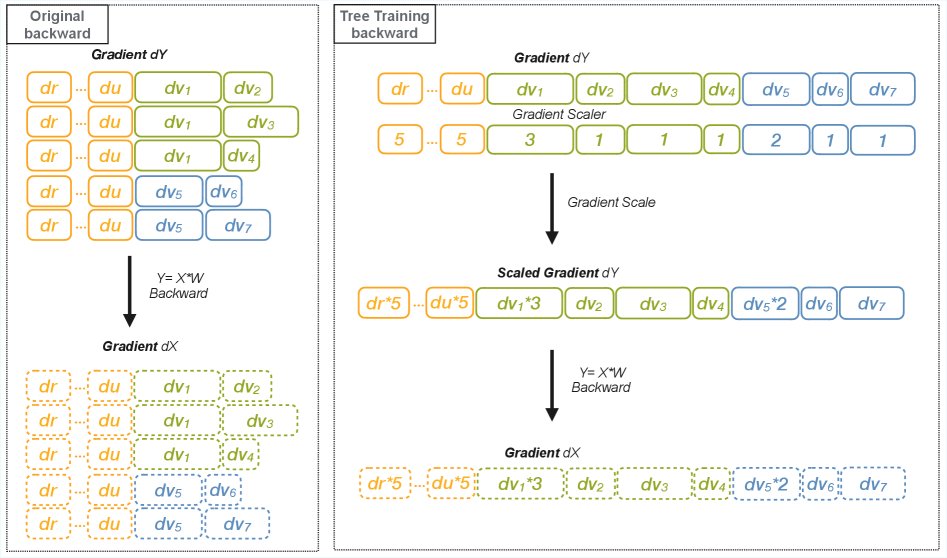
  3. 梯度缩放 (Gradient Scaling): 在反向传播开始时（计算 $dY$ 之后），应用一个梯度缩放器（gradient scaler）。对于每个共享前缀的token，将其梯度乘以它的复用次数（即共享该前缀的轨迹数量）。例如，若一个前缀被5个轨迹共享，其梯度就乘以5。这精确地实现了 $dY_{P}^{ours}=\sum dY^{base}_{p_{i}}$ 的目标，从而保证了全局梯度更新的正确性。

Refer to caption

实验结论

本文在多个Qwen3模型和不同数据分布上验证了Tree Training的有效性。

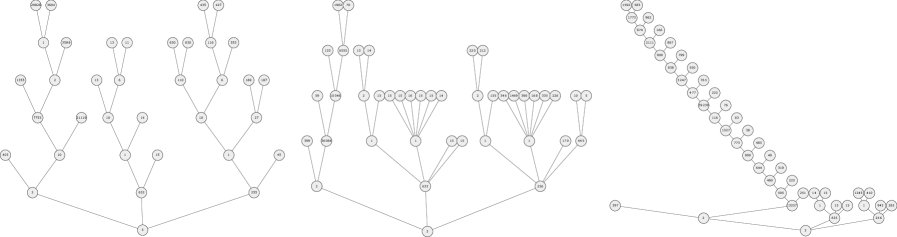
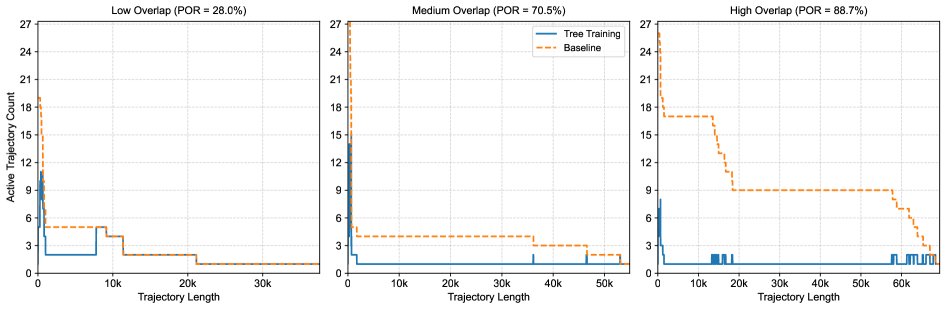
Refer to caption Refer to caption

上图展示了从智能体RL部署中提取的不同前缀重叠率（Prefix Overlap Ratio, POR）的轨迹树，以及Tree Training相对于基线（Sequence Packing）在处理token数量上的节省。POR越高，节省越显著。

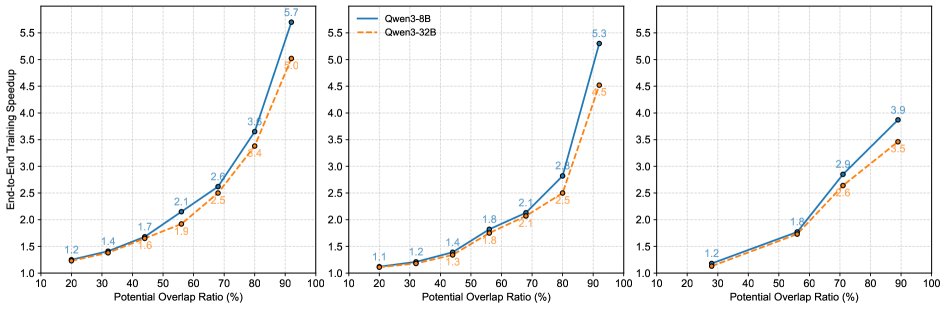
Refer to caption