Why Less is More (Sometimes): A Theory of Data Curation

ArXiv URL: http://arxiv.org/abs/2511.03492v1
作者: Mohammad Pezeshki; Elvis Dohmatob; Reyhane Askari-Hemmat
发布机构: Concordia University; Meta; Mila–Quebec AI Institute

TL;DR

本文建立了一个理论框架，通过推导精确的缩放定律，揭示了在何时以及为何精心筛选（curate）一小部分数据进行训练，会比使用全部数据获得更好的性能，从而解决了“少即是多”与“多即是多”的矛盾。

关键定义

本文的理论分析基于以下关键定义：

参数化率 (Parametrization Rate, $\phi$): 在高维极限下，$d/n \to \phi$，其中 $d$ 是数据维度，$n$ 是样本数量。该比率衡量了问题维度相对于数据集大小的比例。
生成器质量 ($\rho$): 定义为 $\rho := \frac{w_{g}^{\top}Cw_{*}}{\ \mid w_{g}\ \mid _{C}\ \mid w_{*}\ \mid _{C}}$。它衡量了训练数据标签生成向量 $w_g$ 与真实标签向量 $w_*$ 之间的几何对齐程度（余弦相似度）。$\rho \to 1$ 表示一个高质量的生成器（标签噪声低），$\rho < 1$ 则表示一个有缺陷的生成器（存在标签偏移）。
预言机质量 ($\rho_*$): 定义为 $\rho_{*} := \frac{w_{o}^{\top}Cw_{*}}{\ \mid w_{o}\ \mid _{C}\ \mid w_{*}\ \mid _{C}}$。它衡量了用于筛选数据的预言机向量 $w_o$ 与真实标签向量 $w_*$ 之间的对齐程度。$\rho_* \to 1$ 表示一个完美的预言机。
生成器与预言机对齐度 ($\rho_g$): 定义为 $\rho_{g} := \frac{w_{o}^{\top}Cw_{g}}{\ \mid w_{o}\ \mid _{C}\ \mid w_{g}\ \mid _{C}}$。它衡量了预言机与数据生成器之间的对齐程度。

本文方法

理论分析设置

为了在数学上精确分析数据策展的效果，本文构建了一个高维二元分类问题的理论模型。

数据、模型与假设

数据分布: 训练数据 $(x_i, y_i)$ 来自生成分布 $P_g = P_{w_g, C_g}$，而测试数据来自真实分布 $P_* = P_{w_*, \Sigma}$。其中，$w_g$ 和 $w_*$ 分别是生成器和真实分布的标签向量。本文重点分析存在标签偏移 ($w_g \neq w_*$) 且协方差矩阵为单位阵 ($C_g = \Sigma = I_d$) 的各向同性情况。
模型: 本文分析一个线性分类器 $\text{sign}(x^\top \hat{w})$，其权重向量 $\hat{w}$ 通过求解以下岭回归问题得到：
\[\text{minimize } \frac{1}{n}\sum_{i=1}^{n}p_{i}\ell(x_{i}^{\top}w;y_{i})+\frac{\lambda}{2}\ \mid w\ \mid ^{2}, \text{ over } w\in\mathbb{R}^{d}\]
其中 $\ell$ 是平方损失函数，$p_i \in {0, 1}$ 是一个指示变量，表示第 $i$ 个样本是否在策展后被保留。
分析目标: 在高维比例缩放极限（$n, d \to \infty, d/n \to \phi$）下，精确刻画模型的测试误差 $E_{\text{test}}(\hat{w})$。

数据策展规则

本文考虑了两种策展机制，均由一个预言机 (oracle) $w_o$ 控制：

标签无关的策展 (Label-Agnostic Curation): 是否保留样本 $(x_i, y_i)$ 仅取决于其特征 $x_i$ 与预言机向量的投影，即 $p_i = q(x_i^\top w_o)$。例如，“保留困难样本”对应于选择投影值小的样本 ($ \mid x_i^\top w_o \mid \leq \alpha$)，“保留简单样本”则对应于选择投影值大的样本 ($ \mid x_i^\top w_o \mid \geq \alpha$) 。
标签感知的策展 (Label-aware Curation): 样本被保留的条件是其标签 $y_i$ 与预言机的判断 $y_i^o = \text{sign}(x_i^\top w_o)$ 一致，并且满足基于难度的筛选规则 $q(x_i^\top w_o)=1$。这种设置更贴近 LIMO 等方法的实践。

核心理论：何时该筛选，何时该放量

创新点

本文的核心创新在于推导出了测试误差的精确解析表达式（缩放定律），从而将数据策展的效果与生成器质量 ($\rho$)、预言机质量 ($\rho_*$)、数据量 ($\phi$) 等关键参数直接联系起来。这使得从理论上确定最优策展策略成为可能。

设置 #1: 标签无关的策展

定理1 (精确测试误差): 本文首先推导了在标签无关策展下，模型测试误差 $E_{test}(\hat{w})$ 的精确极限表达式。该表达式是一个复杂但完全解析的函数，其变量包括策展策略 $q$ 的四个关键统计量 ($p, \gamma, \beta, \tilde{\beta}$)、生成器质量 $\rho$、预言机质量 $\rho_*$、以及数据参数 $\phi$ 和正则化系数 $\lambda$。

\[E_{test}(\hat{w}) \to \frac{1}{\pi}\arccos\left(\frac{ \mid m_0 \mid }{\sqrt{\nu_0}}\right)\]

其中 $m_0$ 和 $\nu_0$ 是通过随机矩阵理论工具推导出的确定性等价量，依赖于上述参数。

基于此定理，本文进一步分析了在数据充足 ($\phi \to 0$) 且无正则化 ($\lambda \to 0$) 的极限下，何种策展策略能使误差最小化。

定理2 (最优策展策略): 最佳的策展策略取决于生成器的质量 $\rho$：

(A) 强生成器 ($\rho \to 1$): 当生成器质量很高（即训练数据标签噪声很小）时，最优策略是保留困难样本（即靠近决策边界的样本）。这与“少即是多”的观点一致，此时模型已经掌握了任务的基础，需要通过困难样本进行精炼。
(B) 弱生成器 ($\rho < 1$): 当生成器质量较差时，最优策略是保留简单样本（即远离决策边界的样本）。这符合“多多益善”的直觉，此时模型需要从简单的例子中学习任务的基本结构，避免被噪声或错误的困难样本误导。

设置 #2: 标签感知的策展

定理3 (标签感知策展下的测试误差): 本文将分析扩展到了标签感知的策展场景，并同样推导出了测试误差的精确解析公式。其形式与定理1类似，但其中的统计量根据新的策展规则进行了相应调整。这一结果为 LIMO 和 s1 等方法提供了直接的理论支持，解释了为何筛选掉标签错误且困难的样本是有效的。

实验结论

本文通过在合成数据和真实数据集（ImageNet）上的实验，验证了其理论预测，并利用该理论解释了近期大语言模型领域的矛盾发现。

理论预测验证

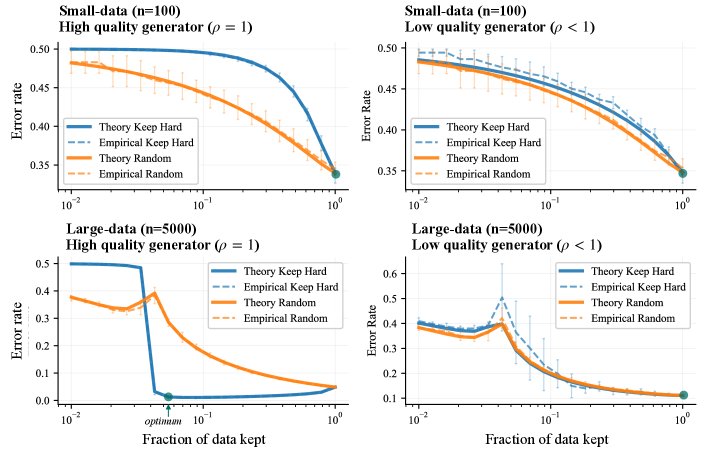
在合成数据上，实验结果完美匹配了理论预测。如下图所示，实验揭示了策展效果的清晰模式：

当数据集较小（上排）或生成器较弱（右列）时，保留所有数据（$p=1$）的效果最好，印证了“多多益善”原则。
仅当数据量充足且生成器强大时（左下角），激进地筛选一小部分困难样本（$p \ll 1$）才能取得最低的测试误差，这正是“少即是多”原则适用的场景。

解释LLM数学推理的发现

本文的理论框架能够统一解释近期在LLM数学推理任务上的矛盾结果。在AIME基准测试上，对于大多数问题，基础大模型是一个强生成器（高 $\rho$），因此，如LIMO和s1所示，激进筛选困难样本的“少即是多”策略能提升平均性能。

AIME 2024 (平均性能)

训练样本数（来源）	性能
0 (基础模型 Qwen2.5_32B)	16.5
114k (Openthinker)	50.2
59k (s1 策展)	53.3
1k (从 59k 中策展)	56.7

然而，当只评估其中最难的一部分问题时，同一个模型相对于这些难题就变成了弱生成器（低 $\rho$）。此时，理论预测“多多益善”是更优策略，实验结果也确实如此：增加训练样本数量可以持续提升模型在难题上的表现。

AIME (难题级别) 性能

训练样本数（来源）	性能
0 (基础模型 Qwen2.5_32B)	1.0
1k from OpenR1-Math	28.4
2k 样本	35.4
10k 样本	52.1
114k (Openthinker)	47.9
1M (Openthinker2)	64.9

ImageNet实验与模型坍塌

在ImageNet上的实验进一步证实了理论的普适性。实验使用一个预训练模型作为生成器和预言机，通过控制其初始训练数据量来调节其“强度”。

策展策略的转换: 如下图所示，当生成器较弱（仅用160K图像训练）时，“保留简单样本”策略更优；而当生成器变强（用1.2M图像训练）后，“保留困难样本”策略变得更有效。这清晰地展示了理论预测的策略转换点。

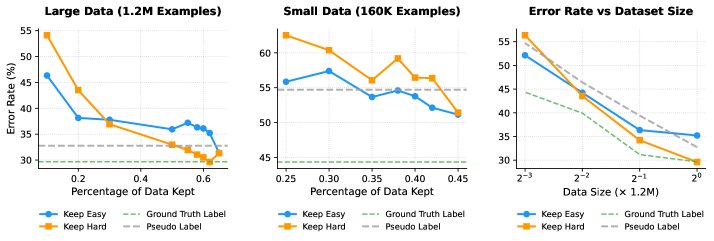
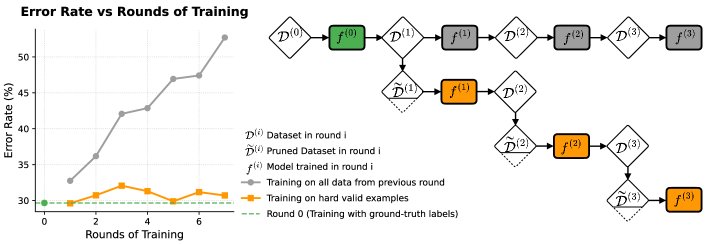
防止模型坍塌: 实验模拟了模型坍塌过程，即模型在自己生成的伪标签上进行迭代训练。结果显示，如果每次都使用全部伪标签数据进行训练，模型性能会迅速下降。相反，如果每次都采用“保留困难且正确”的策展策略，模型性能能够保持稳定，有效避免了模型坍塌。

总结

本文的理论与实验共同证明，数据策展并非一种启发式技巧，而是一种有原则的学习工具。最优的策展策略依赖于具体情境，特别是生成器（或现有模型）相对于目标任务的强弱。在正确的条件下，“少即是多”不仅能提升效率和性能，还能在迭代训练中稳定模型，防止模型坍塌。